Research
Solid State Quantum Optics, Manipulation of Quantum States
|
Two technological advances open the way to observe new many-body effects in confined geometries: (1) quantum dots can be controllably charged by several electrons or holes (2) the photoluminescence spectrum of a single quantum dot can be measured with an energy resolution of few micro electronvolts. With our theoretical approach, we are able to predict the optical characteristics of such combinations of light and charge excitations. |
|
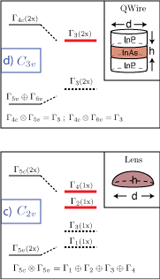
We predict that heterostructure quantum wires and [111] grown quantum dots have a vanishing fine-structure splitting on the grounds of their symmetry, and are therefore ideal candidates to generate entangled photon pairs. We underpin this proposal by atomistic million-atom many-body pseudopotential calculations of realistic structures and find that the vanishing fine-structure splitting is robust against possible variations in morphology. We predicted that in conventional self-assembled quantum dots the exciton lines anticross leading to a lower bound for the fine structure splitting. Singh and Bester, Phys. Rev. Lett. 103, 063601 (2009). |
||
|
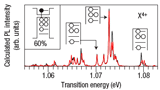
We calculated the photoluminescence spectrum of highly charged self-assembled quantum dots and compared it with experimental results obtained in the group of Prof. Warburton. By the comparison of experiment and theory we could unveil many-body effects not evidenced before. Especially we found
|
||
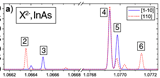 |
The electron-hole exchange interaction leads to a splitting of the excitonic lines into a so-called fine structure that shows a particular sequence of peaks with specific polarization. The polarization and the splitting give detailed information about the spin-configuration of the exciton and charged exciton. Ediger et al., Phys. Rev. Lett. 98, 036808 (2007) (PDF) |
||
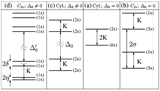 |
We performed the first atomistic calculation of the fine-structure in a self-assembled quantum dot. Our initial emphasis was to understand the underlying physics of the effect and we separated the fine splitting into contributions from atomistic symmetry (C2v symmetry, vs. Td symmetry) and the effect of spin-orbit coupling. Bester et al., Phys. Rev. B. 67, 161306(R) (2003) (PDF) |
Electronic Correlations in artificial atoms
The Coulomb correlation energy describes the energy missing in a Hartree-Fock ground state energy calculation. In other words, it is the part of the ground state energy that makes a description in terms of effective non-interacting entities impossible. It is a truly non-local quantity: the state of an electron at position r, depends on the state of the other electrons at positions r'. From a theoretical point of view, it is a well defined quantity that can be calculated to a high level of accuracy for simple systems. Experimentally, it is not obvious how such a quantity could be isolated from the obervables: the correlation is an inextricable part of the many-body total energy. In the area of "highly correlated materials", the knowledge about the degree of correlation is limited to the fact that these materials elude a proper treatment by theoretical methods that approximate the effect of correlations, such as DFT. The stydy of quantum dots, where a varying number of carriers can be introduced, opens up a possibility to extract the correlation energy from the total many-body energy. This allows us to get a glimpse at this subtle and important quantity and to benchmark our theory.
Ediger et al., Nature Physics 3, 774 (2007).
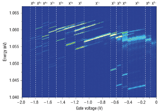
Labud et al., Submitted (2012).
Ab initio molecular dynamics; Photoelectrochemistry
In collaboration with experimentalists in-house (K.-D. Kreuer, Abt. Maier) and Mark Tuckerman at NYU we perform Ab Initio Molecular Dynamics (AIMD) simulations of ionic transport in condensed matter. We have studied the mechanism of proton conduction in phosphoric acid. |
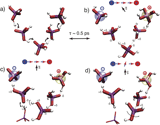 |
Understanding proton transport mechanisms in hydrogen bonded systems remains one of the most fundamental problems in many areas of science ranging from electrochemical energy conversion to biological systems. The molecular level description of this phenomenon involves a number of complex bond breaking and forming processes, which can only be addressed by a self-consistent treatment at the ab initio level, allowing for a dynamical charge redistribution and screening. At present, a plain ab inito molecular dynamic (AIMD) treatment of diffusion process in condensed matter systems is mostly elusive because of the large number of particles and especially the time scales involved. We have pushed AIMD to the present day computational limits for a judiciously chosen system - phosphoric acid - the system with the highest known intrinsic proton conductivity. With this combination we could unveil a microscopic conduction mechanism reminiscent of the earlier notions suggested by von Grotthuss 200 years ago for aqueous proton transport. We find that the strong and highly polarizable H-bonds give rise to a concerted proton motion and the formation of polarized (Grotthuss) chains, never before observed in H-bonded systems. It is the complex interplay between these chains together with "frustrated" network of hydrogen bonds, which is suggested to explain the extremely high proton conductivity of phosphoric acid. The proof that this type of conduction mechanism exists, opens the way for a fresh interpretation of proton transport in general. It is also remarkable that we observe this extreme case of concerted proton motion for the phosphate based system. Phosphates are of fundamental importance for the existence of life, e.g. proton gradient is suggested to be driving the ATP synthesis, with the protons being transported between their source and sink along the phospholipid/aqueous interface. Moreover, the molecular understanding of this mechanism is of great importance for the biological systems and development of new phosphoric acid based electrolytes for fuel cell membranes. L. Vilciauskas et al., Nature Chemistry 4 461 (2012). |
Ultrafst Dynamical Processes
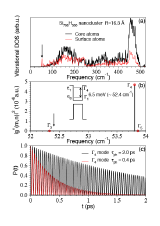 |
Ultrafast Carrier Relaxation via Electron-Phonon Coupling. We establish a methodology that enables us to calculate the electron-phonon coupling matrix elements from ab-initio density functional theory for clusters with up to 1000 atoms. We feed these elements into a density matrix formalism (optical Bloch equations) that allows us to study the time evolution of excited states. Ongoing work includes the study of the coherence of the states. Han and Bester, Phys. Rev. B. 85, 235422 (2012) |
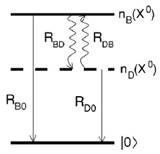 |
Fine-Structure Effects on Carrier Relaxation. The Electron-hole exchange interaction splits the exciton ground state into "dark" and "bright" states. The dynamics of those states depends on the internal relaxation time between bright and dark states (which involves a spin-flip), and the radiative recombination time of the bright states. We calculate the radiative decay rates for monoexcitons and biexcitons in self-assembled and colloidal quantum dots from atomistic correlated wave functions. Narvaez et al. Phys. Rev. B. 74, 075403 (2006) (PDF) |
 |
Auger Cooling in Self-Assembled dots . We calculate the P-shell-to-S-shell decay lifetime of electrons self-assembled InGaAs/GaAs dots due to Auger electron-hole scattering. We find that this relaxation mechanism leads to fast decay of P → S between 1-7 ps for dots of different sizes which compares well to experimental results. We argued that as long as both electrons and holes are present there is no need for an alternative polaron mechanism to explain the lack of phonon-bottelneck. Narvaez et al. Phys. Rev. B. 74, 075403 (2006) (PDF) |
Spin Orbit Effects
|
In collaboration with Alex Zunger and Jun-Wei Luo at the National Renewable Energy Laboratory, we have started to investigate spin-orbit interactions in semiconductors, leading to Dresselhaus and Rashba spin-splittings. Spin splitting is one of the relevant quantity in the context of quantum information science. |
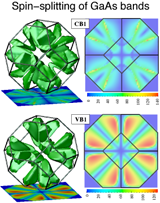 |
Full-Zone Spin Splitting for Electrons and Holes in Bulk GaAs and GaSb. We provide a full-zone description of the Dresselhaus splitting in zinc blende semiconductors by using pseudopotentials, empirically corrected to rectify local density approximation errors by fitting GW results. We find a maximum in the spin splitting of the conduction band close to the [210] direction, at the anticrossing of two conduction bands. Luo et al. Phys. Rev. Lett. 102, 056405 (2009) (PDF) |
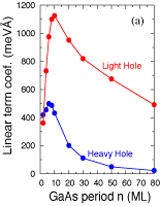 |
Discovery of a Novel Linear-in-k Spin Splitting for Holes in the 2D GaAs=AlAs System. We discover a large linear scaling of valence band states in 2D (Quantum Wells). This scaling emerges from the mixed (heavy- and light-hole) character of the VBM. This discovery of a linear Dresselhaus k scaling for holes in 2D implies a different understanding of hole physics in low dimensions. Luo et al. Phys. Rev. Lett. 104, 066405 (2010) (PDF) |
Entanglement
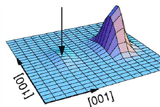 |
2e in a Dot Molecule. Two vertically or laterally coupled quantum dots containing electrons, holes, or an exciton constitute one of the solid structure proposed for the basic gate operations of quantum computing. The key quantities we calculated are the singlet-triplet splitting and the degree of entanglement that can be achieved in a realistic structure. We employed different methods that treat correlations at different level (Hubbard, Heisenberg Models, Hartree-Fock and Configuration Interaction) He et al. Phys.Rev. B. 72, 195307 (2005) (PDF) |
||
|
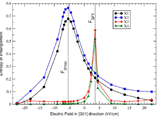
One Exciton in a Dot Molecule. We calculated the degree of entanglement of an optically created exciton and suggested to use an external electric field to tune it. At the critical field, where the entanglement is maximized, we predict a clear optical signature. Details of the physics underlying the tunneling process of holes and electrons have been revealed, especially the role of strain (light-hole tunneling) and a reversal of the bonding-antibonding state order (anti-bonding being lower in energy). Bester et al. Phys.Rev.Lett. 93, 047401 (2004) (PDF) |
Wave Function Imaging
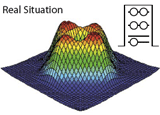 |
Magnetotunneling Spectroscopy (MTS). We extended our method to be able to calculate processes, such as MTS or Near Field Scanning Optical Micorscopy (NSOM). These experimental techniques have the potential to deliver insights into the quantum states, not availbalbe before. We calculated MTS maps and could monitor the effects of (i) correlations, (ii) atomistic symmetry, and (iii) piezoelectricity on the confined carriers and (iv) observe a peculiar charging sequence of holes that violates the Aufbau principle, in collaboration with experimentalists. Bester et al., Phys. Rev. B 76, 075338 (2007) (PDF) |
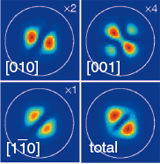 |
Near Field Scanning Optical Micorscopy (NSOM). We calculated the signal expected from NSOM measurements. We show the wave functions of neutral exciton X0 of different polarizations and compare them to those of the biexciton XX0 and the charged excitons X+ and X-. We further show that the exciton X Ph → Pe transition which is forbidden in the far-field photoluminescence has intensities comparable to those of X Sh → Se transition in the near-field photoluminescence. He et al. Phys.Rev.B. 76, 035313 (2007) (PDF) |
Piezoelectric Effects
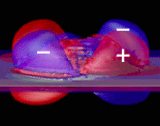 |
In Quantum Dots . The process of self-assembly that underlies the growth of SK-dots is driven by strain. Indeed, the strain present in an SK dot corresponds to a high pressure not atainable in the laboratory setting. Since the III-V semiconductors in zinc-blende symmetry have not inversion symmetry, they exhibit piezoelectric effects. We calculated the effect, including second order terms in strain, on different properties and find it to be small (in InGaAs/GaAs dots) for most of the electronic properties, while it can change the symmetry of wave functions and have a significant effect on polarizations. Bester et al. Phys.Rev.B. 74, 081305 (2006) (PDF) |
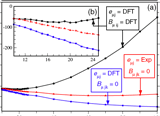 |
Second Order Effect . Using the Berry Phase approach in density functional theory we calculted the second order piezoelectric effect and found it to be as large as the first order effect. These results bare consequences, since the second order effects was neglected until then. We concluded that second order in strain must be taken into account and that the measured piezoelectric coefficients are effective quantities encompassing a large non-linear part. Bester et al. Phys.Rev.Lett. 96, 187602 (2006) (PDF) |
Colloidal Nanostructures
 |
Nano Dumbbells. This was the first step towards the atomistic description of an architecture/assembly of nanostructurs. Two CdTe dots are connected by a CdSe wire. We investigated the localization of the carriers due to chemical effects (band-offsets) and due to correlations. A similar system has been realized experimentally since then. Franceschetti et al. Nano. Lett. 6, 1069 (2006) (PDF) |
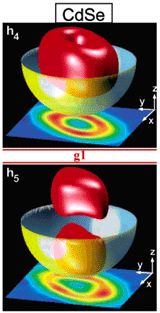 |
Hole Relaxation . We find that in the excitonic manifold derived from the ground state electron and the first 60 hole states there are two energy gaps much larger than the typical LO phonon energy in bulk CdSe. Such gaps can effectively slow down the hole relaxation process, as was found experimentally. We show that they originate from two gaps in the hole spectrum and are therefore a single-particle effect, as opposed to an excitonic effect. The figures shows the square of the wave function (red) of the two hole states, above and below the gap. The yellow shape is there to indicate the geometry of the dot. Califano et al. Nano. Lett. 3, 1197 (2003) (PDF) |
Excitonic Ground States and Phase Diagrams
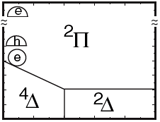 |
Phase Diagrams. We showed that the charging pattern of holes (which shells are occupied in which oder) exhibits unexpected features, notably the skipping of one of the P-shells. We investigated the generality of this result by drawing 2D phase diagrams which describe in a general fashion different charging sequences for different dots. He et al. Phys. Rev. Lett. 95, 246804 (2006) (PDF) |
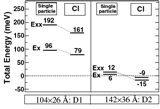 |
Excitonic Ground State. We predict that in InAs/InSb dots (to our knowledge not yet synthesized), due to: (i) Strong electron-hole correlation effects are induced by the spatial proximity of the electron and hole wave functions, and (ii) the lack of strong (exciton unbinding) screening. A biexcitonic should form spontaneously, i.e., without the requirement of light excitation. He et al. Phys. Rev. Lett. 94, 016801 (2005) (PDF) |